Święta geometria Wszechświata

Dawno już nie naskrobałem żadnego ciekawego tekstu, więc już czas najwyższy, żeby nadrobić zaległości. Długo nie musiałem myśleć nad wyborem tematu, gdyż pomysł na napisanie co nieco o tej "materii" chodził za mną od dłuższego czasu. Teraz mam trochę wolnego czasu, więc do dzieła! Dlaczego więc akurat "święta geometria" i co to w ogóle jest? Wbrew pozorom to nie jest temat o matematyce, lecz o otaczającym nas świecie i o nas samych. Jest to temat o wszystkim co istnieje, ale o tym później. Najpierw postaram się napisać krótkie wprowadzenie do tematu, bo napewno nie każdy spotkał się już z tym wcześniej.

Pierwszy raz z tym fenomenem spotkałem się na studiach. Mieliśmy bardzo pozytywnie zakręconego profesora, który prowadził z nami ćwiczenia z matematyki. Człowiek ten potrafił prowadzić zajęcia w taki sposób, że z miłą chęcią przychodziło się, żeby powojować z wzorami i obliczeniami na tablicy, a te łatwe wcale nie były, bo to już wyższa matematyka. Tak czy inaczej, zawsze było ciekawie, bo facet dość często podczas rozpoczynania zajęć rzucał jakiś żart, a potem opowiadał jakąś ciekawostkę ze świata, dotyczącą zazwyczaj matematyki, lecz nie zawsze. I tak oto pewnego razu opowiedział nam o "magicznej" liczbie φ (czyt. "fi") i o zasadzie "złotego podziału", o której napiszę w dalszej części artykułu. Zaciekawiło mnie to bardzo i po powrocie do domu zacząłem szukać czegoś więcej na ten temat. Znalazłem tego bardzo dużo i jeśli mam być szczery, to zadziwił mnie fakt, że nie znałem tematu wcześniej.

Wstęp

Czym jest owa tajemnicza grecka liczba φ?

Właściwie nie jest to liczba, lecz określenie stosunku wielkości jednej liczby do drugiej. Zobrazuję to na przykładzie prostego odcinka, podzielonego na dwie części, tak aby stosunek długości jednej jego części do drugiej wynosił dokładnie tyle ile wynosi wartość liczby φ.

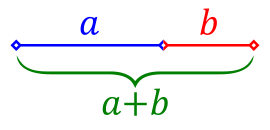
Na obrazku mamy więc odcinek (nazwijmy go c). Odcinek ten podzielony jest na dwie części: a i b. Jednocześnie całkowita długość odcinka c = a + b.

Jak widać, część a jest dłuższa od części b. Jest to tzw. "złoty podział", ale o tym później. Popatrzmy jeszcze raz na długości a i b. A teraz spróbujmy "na oko" określić jaką część odcinka a stanowi odcinek b. Żeby było prościej, pokaże obie długości, jedną pod drugą:

Jak widać dwa odcinki b nie zmieszczą się w odcinku a, na oko w odcinku a zmieści się jakieś 1,6 odcinka b. I tu właśnie doszliśmy do owej magicznej liczby φ, której wartość wynosi w przybliżeniu:

φ = 1,6180339887...

Liczba ta określa w naszym przypadku stosunek długości odcinka a do odcinka b.  

a / b = φ

Poniżej przedstawiam prostokąt podzielony na dwie części za pomocą reguły złotego podziału:

Wiemy już na czym polega złoty podział, więc teraz może słów kilka, po co to komu potrzebne. Otóż taki podział znany był już w czasach starożytnych, gdy zauważono, że stosowanie właśnie takiej, a nie innej proporcji wydaje nam się "wewnętrznie" najbardziej naturalne, najbardziej harmonijne, ale o tym później. Stąd też regułę złotego podziału wykorzystuje się w wielu projektach, zarówno artystycznych jak i architektonicznych. Projekty oparte na złotym podziale wydają nam się naturalne, estetyczne. Jako przykład pokażę poniższe zdjęcia:

 

Jak widać na przykładzie ostatniego zdjęcia, złoty podział nie ogranicza się jedynie do dwóch prostokątów, lecz rozciąga się w nieskończoność na zasadzie - każdy kolejny prostokąt jest mniejszy w stosunku do poprzedniego z zachowaniem proporcji liczby φ, a więc stosunek wielkości każdego poprzedniego prostokąta do wielkości następnego mniejszego = φ. Poniżej prostokąt podzielony zgodnie z zasadą złotego podziału:

Na powyższym przykładzie widzimy coś nowego - spiralę wpisaną w "złoty prostokąt". Czy ta spirala nie wydaje się proporcjonalnie naturalna? No właśnie.

Ale o tym później. Narazie pomęczymy jeszcze temat liczby φ. W tym momencie dochodzimy do bardzo istotnej sprawy związanej ze "złotą liczbą", mianowicie do tzw. ciągu Fibonacciego. Nie wnikając we wzór matematyczny ciągu napiszę jedynie jak wygląda taki ciąg. Otóż jest to ciąg liczb tworzony na zasadzie: "każda kolejna liczba jest sumą dwóch poprzednich liczb". Poniżej przedstawiam taki ciąg zaczynający się od zera:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... (i tak do nieskończoności)

Jak widać, reguła Fibonacciego jest tutaj zawarta - każda następna liczba ciągu  to suma dwóch poprzedzających ją liczb. Liczby wchodzące w skład takiego ciągu nazywa się liczbami Fibonacciego.  

No dobrze, ktoś zapyta - ale co to ma wspólnego z liczbą φ ? Otóż wszystko. Spójrzcie jeszcze raz na podzielony prostokąt znajdujący się kilka linijek wyżej (ten ze spiralą). Wyobraźmy sobie teraz, że każdy z tych prostokącików ma jakieś tam pole powierzchni. Oczywiście im większy prostokąt tym większe pole. A teraz spójrzmy na obrazek poniżej, na którym owe pola powierzchni zostaną pokazane:

Popatrzcie na liczby na prostokącie, a następnie na liczby z ciągu Fibonacciego. Wygląda znajomo? No właśnie. Stosunek każdej kolejnej liczby do liczby poprzedniej w ciągu Fibonacciego to właśnie liczba φ! Można sobie to samemu sprawdzić na kalkulatorze.

Jako dowód: 8/5=1.6, 5/3=1.6, 3/2=1.6....można sprawdzić na własnym kalkulatorze. No dobrze, wiemy więc już teraz co nieco o tym, czym jest liczba φ i jaki związek ma ona z ciągiem Fibonacciego, tak więc wprowadzenie do tematu uważam za zamknięte. Tak, tak - to było jedynie wprowadzenie, teraz zaczynamy o tym co najciekawsze :)

Złota proporcja w życiu.

Tak jak napisałem na wstępie, liczba φ i reguła "złotego podziału" były znane już w starożytności. Teraz napiszę o tym trochę więcej. Już starożytni architekci wykorzystywali złotą proporcję do tworzenia swoich budowli. Wykorzystano ten podział m.in. podczas budowli Akropolu, liczbą φ fascynował się również sam Euklides, który był nią podobno wręcz zauroczony, ze względu na jej cudowne właściwości. Złotego podziału używał w swoich pracach nawet sam Leonardo da Vinci. 

Wystarczy spojrzeć na jego "Człowieka witruwiańskiego". (zdj. poniżej)

Złoty podział był wykorzystywany na przestrzeni wieków przez wielu znanych budowniczych. Wiele znanych budowli powstawało w oparciu o jego zasadę. Można tu wymienić np. Pantenon, czy Wielki Meczet. Również w czasach obecnych, każdy szanujący się architekt wykorzystuje złote proporcje w swoich projektach. Złoty podział jest jednak przede wszystkim wykorzystywany w sztuce. Jest rzeczą absolutnie fenomenalną, że my jako ludzie, mamy w swoich głowach zakodowaną wrażliwość właśnie na "złoty podział". Kształty oparte na tej regule wydają nam się ciekawsze od kształtów nie zawierających w sobie złotego podziału. Jest to jakby matematyczny, naturalny wzór na piękno i harmonię.  Były na ten temat prowadzone nie jedne badania, często przez znanych i cenionych psychologów. Badania te potwierdziły tezę, iż jesteśmy na swój sposób "zaprogramowani" na postrzeganie właśnie takich, a nie innych proporcji i kształtów. Nic więc dziwnego, że zasadę tą wykorzystuje się w sztuce i to od bardzo dawna. Malarze tacy jak Leonardo da Vinci, czy Salvadore Dali z powodzeniem wykorzystywali zasadę złotego podziału w swoich dziełach.

Co ciekawe, reguła złotego podziału wykorzystywana była również w...muzyce. Badacze odkryli, iż nawet Chopin wykorzystywał tą regułę w komponowaniu swoich utworów. Mało kto zdaje sobie z tego sprawę, ale również w ekonomii i na rynkach finansowych reguła ta ma bardzo szerokie zastosowanie. 

Najciekawsze jest jednak zastosowanie reguły złotego podziału nie przez człowieka, lecz przez...Wszechświat.

Czy Bóg to matematyk?

Dochodzimy do najciekawszej części artykułu, czyli do występowania złotej proporcji we wszystkim co nas otacza. Jest to o tyle ciekawe, bo liczba φ wydaje się występować absolutnie w każdym aspekcie budowy naszego świata. Wydaje się być uniwersalną liczbą Natury. 

Na początek popatrzmy na rysunek pentagramu. Symbol ten określany jest mianem "magicznego". Popatrzmy na niego:

Co się okazuje? Okazuje się, że wszystkie ramiona tego "magicznego" symbolu przecinają się na zasadzie "złotej proporcji".

 A teraz weźmy do ręki jabłko, przekrójmy je i spójrzmy:

To dopiero początek. Pamiętacie spiralę opartą na złotym podziale, którą pokazałem przy okazji opisywania liczb Fibonacciego? Jest to tak zwana spirala Fibonacciego. Dla przypomnienia spójrzmy na nią jeszcze raz:

Potocznie używa się też innych nazw, takich jak "złota spirala", czy "boska spirala". Za chwilę przedstawię Wam jak właśnię TĄ spiralą operuje przyroda, jednak na początek, żeby dać Wam do myślenia, przedstawiam zdjęcie naszej własnej Galaktyki:

Przypomina Wam to coś? No właśnie. Spójrzmy jeszcze raz:

Matematyka zawarta w złotej proporcji wydaje się być magicznym wzorem Wszechświata, począwszy od skali makro, aż do skali atomowej. Uniwersalna liczba φ wydaje się więc być dowodem na matematyczną budowę wszystkiego. Powróćmy jednak do samej spirali Fibonacciego. Jak się okazuje, spirala ta wręcz rządzi naszym życiem i wszystkim tym co nas dookoła otacza. Zacznijmy może od roślin. Jak wykazały badania nad nimi - spirala Finobacciego jest znana większości roślin. Wyznacza ona bowiem kierunek ich wzrostu. Tak, tak - rośliny rosną w oparciu o ten właśnie matematyczny kształt, co przedstawia poniższa animacja, wszak jeden obraz pokaże Wam więcej, niż tysiąc słów:

W biologii znany jest termin "filotaksja", który oznacza to samo co "ulistnienie". Termin ten opisuje sposób w jaki liście rośliny rozrastają się wokół pnia. Filotaksja mówi m.in. tak:  

"Gdyby ponumerować gałęzie zgodnie z wysokością na jakiej wyrosły wówczas okaże się, że liczba gałęzi sąsiadujących pionowo jest liczbą Fibonacciego, a ponadto liczba gałęzi pomiędzy gałęziami sąsiadującymi pionowo również jest liczbą Fibonacciego. Jeśli spojrzymy w dół na roślinę wówczas zauważymy, że liście wzajemnie się nie zasłaniają, co umożliwia maksymalne wykorzystanie energii słońca oraz zebranie największej ilości deszczu, który spływa po liściach do pnia i korzenia."

Okazuje się więc, że spirala Fibonacciego pozwala uzyskać roślinie kształt idealny. A więc do wspomnianych wcześniej walorów estetycznych dochodzi nam jeszcze jedna właściwość liczby φ, tym razem pozwalająca na uzyskanie optymalnego dla życia i rozwoju rozrostu.

Popatrzmy teraz na kwiat słonecznika, okazuje się, że ilość lewo i prawo-skrętnych spiral odpowiada kolejnym liczbom ciągu Fibonacciego, tutaj odpowiednio 34 i 55.

Popatrzmy jeszcze raz, tym razem w porównaniu z wygenerowaną komputerowo spiralą:

Jak widać, przyroda opiera się całkowicie na matematycznym modelu uwzględniającym nic innego, jak tylko ciąg Fibonacciego. Nie dotyczy to jedynie ułożenia ziarenek słonecznika, ani sposobu w jaki roślince wyrastają liście, dotyczy to absolutnie WSZYSTKIEGO, co potocznie nazywamy "przyrodą". Chcecie więcej? Proszę bardzo, poniżej następne przykłady, odpowiednio - stokrotka i szyszka:

Pójdźmy teraz bardziej w trzeci wymiar, poniżej zdjęcie kalafiora:

A teraz zadajmy sobie pytanie - dlaczego róża wydaje nam się tak pięknym kwiatem?
Odpowiedź przedstawiam poniżej:

Zostawmy na chwilę rośliny i pójdźmy w stronę zwierząt. Każdy chyba widział na własne oczy muszlę. Budowa muszli to nic innego, jak spirala Fibonacciego, poniżej zdjęcia:

 I jeszcze małe porównanie do Drogi Mlecznej, czyli naszej rodzinnej galaktyki:

A tu poniżej rozgwiazda, której budowa oparta jest na pentagramie, który z koleji oparty jest na złotych proporcjach:

Przykładów można by wymieniać miliony, bo złote proporcje występują wszędzie, na każdym kroku. Mamy je wszędzie, widzimy wszędzie dookoła nas, tyle tylko, że rzadko się nad tym tak naprawdę zastanawiamy. Gdy widzimy coś pięknego, to zazwyczaj nie rozkładamy tego na matematyczne czynniki, tylko stwierdzamy, że po prostu to coś jest piękne, lub nie. A szkoda, bo może warto czasem spojrzeć na świat właśnie pod takim kątem, choćby z czystej ciekawości, żeby przekonać się na własne oczy o tym wszystkim, o czym tutaj piszę.

W dalszej części artykułu przejdziemy do budowy płatków śniegu i kryształów, ale dopiero później, gdyż najpierw będę musiał napisać krótkie wprowadzenie odnośnie fraktali i brył platońskich. Narazie zostańmy więc w temacie złotego podziału. Było krótko o roślinach, było krótko o zwięrzętach, więc może teraz trochę o człowieku. Nasze ciała są w całości zbudowane zgodnie z regułą złotego podziału. Nie widzimy tego, nie mierzymy, a mimo to tak właśnie jest,  co za chwilę przedstawię. Zacznijmy od cząstek najmniejszych, na początek budowa łańcucha DNA, którego spirala "zakręca" na zasadzie właśnie spirali Fibonacciego.

A teraz nasz szkielet - wszystkie nasze kości zbudowane są na zasadzie złotego podziału. Zacznijmy od tego co każdy widzi przed sobą, czyli naszych własnych dłoni. Spójrzcie na swoje dłonie, zegnijcie palce i popatrzcie jak kolejne kości w palcu zmniejszają proporcjonalnie swoją długość. Aparatu Roentgena zapewnie pod ręką nie macie, więc proszę bardzo, tutaj pokazane jest to dokładniej:

Przejdźmy teraz trochę wyżej, do przedramienia i ręki:

Jak widać na powyższych zdjęciach, ludzka ręka "skraca się" w myśl zasady złotego podziału. Nie dotyczy to jedynie naszych rąk, spójrzmy np. teraz na nasze nogi i w ogóle na całą ludzką sylwetkę. Odległości od kolana do biodra, od biodra do szyji i od szyji do czubka głowy zmniejszają się na zasadzie złotego podziału, podobnie jak odległość od biodra do kolana w stosunku do odległości kolana do stopy:

Popatrzmy też na konstrukcję naszej twarzy, oczywiście każdy ma inną, jedni bardziej, drudzy mniej proporcjonalną, jednak ogólna zasada zawsze jest zachowana. Odległości od brody do środka ust, od środka ust do linii oczu i od linii oczu do czubka głowy rosną w stosunku złotego podziału. U zdrowego człowieka tak jest zawsze, niezależnie od tego jak bardzo koślawą ma twarz ;)

No dobrze, na tym w skrócie zakończymy ten temat i przejdziemy do fraktali. 

Fraktale.

Czym są fraktale? Z nazwą zapewne każdy się spotkał, jednak zapewne nie każdy wie co to jest, jak powstaje i do czego służy. Postaram się to najprościej jak potrafię wytłumaczyć. Tak żeby każdy zrozumiał.

W skrócie - fraktal to samopowtarzający się wzór, który nie ma końca, maleje w nieskończoność. Formalnie wg definicji fraktalem nazywamy obiekt, którego mniejsze elementy mają taką budowę jak większe, tj. różnią się jedynie skalą, natomiast wszystkie proporcje zostają zachowane. Przykładem na zrozumienie może posłużyć rosyjska "matrioszka". Mamy tam więc dużą babę, w niej mniejszą, ale taką samą, w niej jeszcze mniejszą i tak dalej i tak dalej. Tyle tylko, że ze względu na fizyczne ograniczenia w końcu dojdziemy do tej "najmniejszej" babeczki. Z prawdziwymi fraktalami jest o tyle inaczej, że zmniejszać możemy je w nieskończoność, a każda ich część będzie wciąż taka sama, tyle że coraz mniejsza. Budowę wzoru fraktalnego (tutaj fraktal Mandelbrota) przedstawia np. poniższa animacja:

Na powyższej animacji przedstawiłem fraktal Mandelbrota, 

natomiast na poniższej przedstawię prostszy - fraktal Kocha:

Animacja pokazuje sposób tworzenia fraktala Kocha. Zasada jest prosta. Rozpoczynamy od trójkąta równobocznego, następnie na każdym jego boku opisujemy kolejny trójkąt równoboczny, o boku równym 1/3 boku trójkąta na którym go opisujemy, na nim następny i następny i tak w nieskończoność...Jak widać fraktal nie ma końca, robiąc jego zbliżenie wciąż będziemy dochodzić do coraz mniejszych i mniejszych trójkątów i tak bez końca. A dlaczego piszę o fraktalach? Dlatego, że fraktale w postaci naturalnej nadzwyczaj często występują w przyrodzie, mimo iż jest to twór czysto matematyczny.

Gdzie więc w przyrodzie występują fraktale? Widzimy ich miliardy podczas pierwszego lepszego opadu śniegu. Popatrzmy na płatki śniegu w przybliżeniu:

Kryształki wody to najzwyklejsze w świecie fraktale. Jak widać przyroda naprawdę kocha matematykę. Oczywiście płatki śniegu to nie jedyne obiekty, które mają budowę fraktalną. Taką budowę wykazuje ogromna ilość obiektów nas otaczających, w tym - my sami, ale o tym za chwilę. Popatrzcie na drzewa i ich gałęzie - mają budowę fraktalną. Popatrzcie na pasma górskie i występujące na nich mniejsze górki i wzniesienia - mają budowę fraktalną, przyjrzyjcie się swojemu układowi krwionośnemu (w wyobraźni) albo popatrzcie na kwiaty - to samo. Fraktale są wszędzie. Jako ciekawostka - spójrzmy teraz na porównanie rozkładu neuronów w ludzkim mózgu z rozkładem galaktyk we Wszechświecie:

Czyżby wszystko samopowstarzało się w nieskończoność? Od skali makro, aż do skali mikro? Wiele na to wskazuje. A jeśli tak jest, to oznacza to, że żyjemy w jednym wielkim fraktalu, który maleje do nieskończoności, a my sami jesteśmy jedynie małym obrazem, kopią czegoś większego. Podobnie możemy porównać elektrony krążace wokół jąder atomów z planetami krążacymi wokół Słońca i tak dalej i dalej.... Czyżby nasz Wszechświat był jednym wielkim mózgiem, w którym żyjemy? Kto wie.  Faktem jednak jest, że geometria fraktalna przez wieki pozostawała poza zasięgiem metod badawczych, a to ze względu na swoją złożoność. Teraz, w dobie komputerów i lepszych metod badawczych naukowcy powoli zaczynają dotykać tematu fraktali. Co więcej, fraktale już od pewnego czasu zaczęły być wykorzystywane w wielu dziedzinach życia, nie tylko w sztuce, ale i w nauce.

Bryły platońskie.

Na sam koniec, jeszcze co nieco o tzw. bryłach platońskich, których również jest pełno w przyrodzie i w ogóle w całym Wszechświecie. Co to są bryły platońskie? 

Otóż są to w rzeczywistości wielościany foremne i jest ich dokładnie pięć. Nazywa się je bryłami platońskimi dlatego, iż to właśnie Platon doszedł do wniosku, że wystarczy dokładnie 5 takich brył, aby można z nich było zbudować wszystko co nas otacza. Bryły te to odpowiednio: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan.

Według definicji, bryłą taką można nazwać jedynie taki obiekt, którego ściany są przystającymi wielokątami foremnymi, w każdym wierzchołku zbiega się jednakowa liczba ścian oraz gdy jest to bryła wypukła.

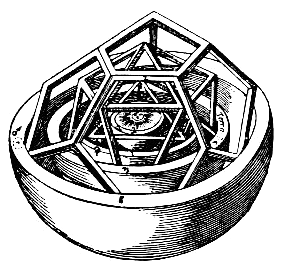
Co ciekawe, Platon wierzył, że budowa całego Wszechświata oparta jest właśnie na tych 5 podstawowych bryłach. Co jeszcze ciekawsze, w XVII wieku niemiecki astronom - Johannes Kepler wykorzystał bryły platońskie do swoich obliczeń kosmologicznych. Chyba każdy z Was choć raz widział model Układu Słonecznego wykonany przez Keplera w oparciu właśnie o bryły platońskie. Jeśli nie, to przypominam:

A tu zbliżenie na wewnętrzną jego część:

No dobrze, model jak model, ładnie wygląda, ale co on tak naprawdę przedstawia? Już śpieszę z wytłumaczeniem. Otóż Kepler odkrył pewną ciekawą prawidłowość w ruchu planet wokół Słońca. Odkrył on mianowicie, że jeśli na sferze (kuli) o promieniu orbity Merkurego opisać platoński ośmiościan, a na nim opisać następną sferę (kulę), to promień tej większej kuli odpowiadać będzie promieniowi orbity Wenus. Idąc dalej - jeśli na tej drugiej kuli opisać dwudziestościan, a na nim kolejną kulę to jej promień odpowiadać będzie promieniowi orbity Ziemii. I tak dalej dla następnych brył platońskich i planet. Dwunastościan dla Marsa, czworościan dla Jowisza, sześcian dla Saturna.

Co ciekawe, bryły platońskie występują wszędzie dookoła, w całej przyrodzie i również podobnie jak w przypadku złotego podziału, spirali Fibonacciego i fraktali - widzimy je przez cały czas, tylko nie zdajemy sobie z tego sprawy. Wystarczy np. spojrzeć na kryształy i ich kształty.

Poniżej kilka kryształów:

 

Na zakończenie pokażę Wam małą ciekawostkę. Otóż wielościany foremne nie dotyczą jedynie trzech wymiarów. Matematycznie można rozpisać je do nieskończonej ich ilości. Jest to niewyobrażalne dla naszego postrzegania i naszych zmysłów, które potrafią ogarniać jedynie 3 wymiary przestrzeni, a jednak - obiekty wielowymiarowe to matematyczny fakt.

Poniżej 4-wymiarowy hipersześcian, czyli popularny tesserakt:

Hipersześcian zagrał też "tytułową rolę" w drugiej części filmu "Cube", czyli "Cube 2: Hypercube".

Zakończenie i podsumowanie.

Wiem, że artykuł wyszedł dość długi, ale uwierzcie mi proszę, ja jedynie "liznąłem" temat. Powstała o tym masa książek, a i w samym internecie znaleźć można multum informacji. Ten artykuł to jedynie wprowadzenie do tematu, jeśli kogoś to zainteresowało to poszuka sobie więcej informacji na ten temat. Mam tylko nadzieję, że chociażby z jedną osobę udało mi się zaciekawić tym fascynującym tematem.

Podsumowując: jak widać przyroda zadziwia, a matematyka jest wszędzie. Nie ma tutaj żadnego chaosu, wszystko to co nas otacza jest harmonicznie zorganizowane i w matematyczny sposób uporządkowane. Na język ciśnie się więc pytanie - czy to wszystko powstało przypadkiem, czy miało swojego architekta?

Jeśli Bóg istnieje, to musi być z Niego naprawdę niezły matematyk. 

Marcin Szczygliński

06.11.2012

(kopiowanie zezwolone jedynie za podaniem autora i źródła)